2024 NCME Presidential Address: Challenging Traditional Views of Measurement
Abstract
This article is adapted from the 2024 NCME Presidential Address. It reflects a personal journey to challenge traditional views of measurement. Considering alternative viewpoints with an open mind led to several solutions to perplexing problems at the time. The article discusses the culture-boundedness of measurement and the need to take that into consideration when designing tests.
Challenging Traditional Views of Measurement
In this article, based on my 2024 NCME Presidential address, I want to talk about some of the encounters throughout my professional life that led me to challenge traditional conceptions of measurement. I also want to highlight some key results I was able to obtain by paying attention to those challenges. A lot of it is anecdotal, and it may seem disconnected at times, but I will try to tie it together at the end. I will warn you in advance, though: this is not meant to be a short course in measurement.
I will begin my journey in elementary school, when I attended a small inner city school with few resources. I often wondered how some students could still thrive in that environment while others languished. In the summer before sixth grade, I decided to devote my career to helping students that fell through the cracks of the educational system. I decided at that moment that I wanted to study psychology. Throughout junior high school and into high school, I read whatever I could find about psychology.
The Study of Psychophysics
I was fascinated by the psychophysicists, who attempted to bring the rigor of the physical sciences to the measurement of human perception. Ernst Weber collected data on the just noticeable difference, which he described as the smallest difference between two physical stimuli that a person could perceive (Fechner, 1966). He discovered that delta-R, the amount of stimulation that needed to be added to stimulus R to produce a just noticeable difference, was a constant proportion of R. Gustav Fechner, relying on Weber's experiments, found that the relationship between a psychological sensation, S, and a physical stimulus R is logarithmic. He believed that we could thereby derive psychological units of measurement from the physical units with which the stimuli themselves are measured (Stigler, 1986). It was very aspirational.
The problem is that, although we can think of stimuli as being built of multiple components, many people argued that sensation is not. Rather, we experience a thing in its totality. Gestalt psychology grew out of this tradition, as a counterpoint to the elementalism that psychophysicists and early experimentalists espoused (Baker, 2012). Wertheimer demonstrated this principle in a set of experiments in which he found that, under the right conditions, people tended to perceive two alternately flashing bars as one bar moving from side to side (Smith, 1988). The human mind wants an organized, structured whole. The “Gestalt,” or form, is primary, and the parts derive their meaning from that whole. For example, we hear a melody first, and only then do we start to discern the individual notes in that melody.
In his book, Principles of Gestalt Psychology, Koffka (1935) said it this way: “It has been said: The whole is more than the sum of its parts. It is more correct to say that the whole is something else than the sum of its parts, because summing is a meaningless procedure, whereas the whole-part relationship is meaningful” (p. 176). I was fascinated by this discussion. Years later, I would come to appreciate it even more when I began to work on testing programs that included essays. Sometimes the essays were scored in an analytic, elemental way, looking for and scoring particular details within the essays. Other times, readers would use a holistic approach: reading, reflecting on and appreciating, and then scoring the entire essay. These two methods of scoring yield appreciable differences.
In college, I buried myself in psychology. We learned experimental psychology in the tradition of Wundt and Titchener, replicating Weber's experiments and testing Weber and Fechner's laws. At the same time, I was pursuing my passion of studying segments of the population who did not always respond well to traditional modes of learning. We also learned about levels of measurement, introduced by Stevens (1946). He was part of a committee of the British Association for the Advancement of Science, right around the time Koffka's book was published. They debated for 8 years whether it was possible to measure human sensation, never reaching a conclusion. Stevens thought the real issue was the meaning of measurement, so he set about rigorously defining different scales and the sets of permissible mathematical operations for each. We learned in statistics class, for example, that we could only compute means and standard deviations and parametric statistics, like Pearson's correlation, if we had at least interval level data. For ordinal or nominal data, we needed to use their nonparametric counterparts, like Spearman's correlation (see Table 1). I embraced this readily, because I was very happy to have rules to follow. But then again, I was only an undergraduate.
| Scale | Empirical Operations | Permissible Transformations | Permissible Statistics |
|---|---|---|---|
| Nominal | Equality | One-to-One | Counts, Mode, Contingency |
| Ordinal | Greater or Lesser | Monotonic Increasing | Median, Percentiles |
| Interval | Equality of Differences | Linear | Mean, SD, Correlation |
| Ratio | Equality of Ratios | Multiplicative | Coefficient of Variation |
Is Level-Headedness a Good Thing?
In graduate school, I began to scrutinize what I had been learning for the last 4 years. During that time, I was administering, scoring and compiling data from IQ tests. I was told that scores from psychological tests like this were ordinal at best, yet I noticed that the score scale derived its meaning by subtracting the mean from the original scores and dividing the difference by their standard deviation.
When it came to statistics, I also discovered that much of what I had heard and read was a misinterpretation of Stevens. For example, I was taught that we should use Pearson's product-moment correlation only for interval data, and Spearman's rank-order correlation for ordinal data. But Spearman's correlation is just Pearson's coefficient applied to ranked data. It didn't make sense. When I actually read Stevens’ (1946) paper in graduate school, I realized that he thought Spearman's correlation was also only appropriate for data that were at least interval level. And yet we applied it to ranks. Stevens made no sense to me either.
I was also still doing hard-core experimental psychology, running rats in mazes. I kept reading about inconsistent results stemming from the outcome measure chosen by the researchers. If they analyzed running speed in feet per second, they got one result. If they chose number of seconds to the target, they got a different result (Anderson, 1961). Same rat, same runway. Why the difference? To me, this seemed a lot more important than levels of measurement, which I viewed as an arbitrary imposition on my data.
At some point, I did a quick thought experiment. Suppose I stood at the finish line of a race and assigned consecutive numbers to runners as they crossed. What level of measurement would these numbers represent? If I asked the runners to line up in order behind me at the water fountain, the numbers could represent the number of people between them and the water fountain. That would be at least interval measurement. If the numbers represented their finishing order, that would be ordinal measurement. If we used the numbers to assign the runners to tables at the banquet, then the numbers would only represent a nominal level of measurement. But they are all the same numbers. It seemed to me that it is not so much the numbers themselves, but the meaning we assign them. I figured we could do to those numbers as we will, so long as our interpretations were in line with our original meaning. I later found vindication for this belief in an article by Zumbo and Zimmerman (1993).
“But you can't multiply ‘football numbers,’” the professor wailed. “Why, they aren't even ordinal numbers, like test scores.”
“The numbers don't know that,” said the statistician. “Since the numbers don't remember where they came from, they always behave just the same way, regardless” (p. 751).
The statistician then formed a confidence interval to demonstrate that it was highly unlikely that the Freshman numbers were a random sample from the population. The professor tried to prove the statistician wrong. But indeed, after a billion samples, the professor only drew two samples outside of the statistician's confidence interval.
At that moment, I determined that I needed to be a quantitative methodologist, not a clinician. Interestingly, when I first went to work at ETS, my office was in Lord Hall. When I later returned to ETS, my office was next to Lord Library. Fred is my hero. He reinforced in me the principle that I should not just do a thing because that is what everyone else does. I should convince myself that it is the right thing to do. Or, I should do something different.
Worth the Weight
Having made the momentous decision to become a methodologist, I studied quantitative psychology and statistics. For my first teaching assistantship in the program, I worked with a professor who was a graduate from Moscow State University. I learned very quickly that he did not think like I did. When he saw the course syllabus, he asked me, “Homework is worth 30%, the Midterm exam is worth 30%, the Final exam is worth 40%. What does that mean?” So I asked him, “What do you mean, ‘what does that mean?’?” He said, “Is it the proportion of variance in the composite explained by each component, is it the loading on the first principal component, or what?”
I explained that we should find the proportion of earned points for each piece of work, multiply it by the assigned percentage, and add them up. He said, “Oh., okay… Why would you do that?” He simply could not understand why it made sense to build a final grade this way. This conversation made me wonder why we do things this way. I began to question how we assign weights to scores when we create composites, and how we assign meaning to the weights. For example, do we use the raw scores, or do we standardize everything first? Are the weights the actual coefficients that we multiply things by, or are they the relative contributions of each part to the total?
Later, when I was designing the composite for a multiple-choice test with essay, I remembered that conversation and used it as the basis for deriving several key equations that helped solve pressing problems of the day. First, how to explain the essay weight? Second, how to make it easy to combine any essay with any multiple-choice section? Third, how to make sure that all the composites were on the same scale? Based on the conversation with my professor from graduate school, I derived a system for solving all these problems by showing the relationships among various ways of defining weights (Walker, 2005). Previously, we needed to combine every multiple-choice (MC) section with every essay separately and then scale the composite to the MC section to place it on the MC scale. With multiple essays, this could take a long time. Using the derived method, we could combine any multiple-choice section with any essay section quickly and easily.
Those questions about the syllabus from my Moscow State University professor urged me to think more broadly about optimal weighting of section scores in a test with multiple parts. What do we mean by optimal? We could choose weights to satisfy any number of criteria. And those weights will of course influence the meaning of the composite score. Criteria may be related to reliability or validity concerns. It can be difficult to define what we mean by optimal, as we often must deal with competing interests. For example, do we care more about content-related issues? Or are we more interested in psychometric properties? Often the solution involves some trade-off between the two, so that we can please multiple stakeholders with different priorities.
My colleagues and I (Ma et al., 2006) decided to brainstorm different ways we could determine weights for a test. We started with a language test with four sections: Reading, Listening, Speaking, and Writing. The plan was to standardize all the section scores and weight them equally, to reflect the fact that all four components of language are equally important. We thought of at least eight other ways to determine weights. The original plan involved assigning equal weight to each section. We could also choose weights based on the amount of time examinees spent on each section, which might add surface credence to the authenticity of the score. Test takers might like this better. We could give equal weight to each scored point or to each item. If the point allocations reflect a proportional sampling from the domain of possible items that measure the construct of language ability, then this makes sense. We could maximize composite reliability or similarly, minimize the composite score standard error of measurement. These strategies should generate very similar or equivalent outcomes. We could assign equal weight to each “effective score point” on the test (Livingston & Lewis, 1995). Effective test length is related to reliability. For a given number of test items, the more reliable the test the greater its effective test length, so this method gives more weight to longer, more reliable sections. We could maximize the composite score variability. To do this, we give the greatest weight to the sections with the greatest variances. The resulting composite score will maximally separate the examinees. I should mention here that we can always increase composite score variance by using larger weights for everything. To control for this, we made sure that the weights for each of these criteria summed to one. We can maximize the proportion of shared variability in the composite score. This goal considers the intercorrelations among the section scores as well as their variances and will tend to assign the greatest weight to the sections with the largest intercorrelations. The resulting composite will explain the largest proportion of total variability in the collection of section scores. This is my professor's first-principal-component solution. Finally, we can maximize the correlation with some outcome measure or other criterion of interest. This goal is concerned with predictive or construct validity.
Figure 1 shows the results of applying the various weights. The section weights are represented by the heights of the components within the bars. Each bar lists writing at the top, followed by speaking, reading, and listening. The composites are listed from left to right in descending order of reliability. Maximum reliability is of course the most reliable, as are minimum standard error and weighting by effective test length (which is related to reliability). Maximizing the variability, on the far right, resulted pretty much in a listening test. Here's something that surprised us: Using the first principal component (to maximize shared variance) gave nearly equal weight to each section. That was comforting, because test developers wanted to give equal weight to everything to begin with.
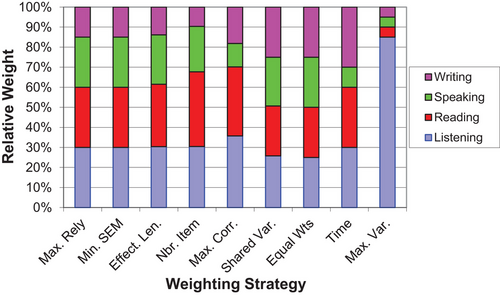
The most important lesson my colleagues and I learned from this exercise was not just to take the first solution that came to mind because it was easy, or expected, or obvious. Instead, we explored multiple possibilities. We realized that different weights used to form a composite should align with the test's purpose. We had to balance psychometric and content concerns, evaluate weights based on relevant criteria, and find the best balance among competing alternatives. In this case, it was relatively easy, because many composites yielded similar reliabilities. Still, each composite tells a slightly different story. And all of this was prompted by a comment by my professor so long ago that got me to question convention.
Essay Reliability
I remember my very first assignment as a psychometrician. It was a mixed format test with multiple choice items and an essay. I noticed that clients, and also some psychometricians, thought the reliability between raters was the reliability of the essay. I sensed that we can always get perfect rater reliability by adding enough raters. But the upper limit of essay reliability is less than that. I was trying to think of a good way to illustrate this. At the same time, I was taking a course on Markov Chain Monte Carlo estimation. In one lecture, the professor gave us some information that triggered an idea. I quickly drew the diagram in Figure 2 and formulated a story (Walker, 2007).
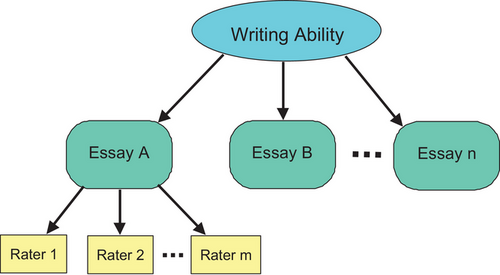
Suppose we want to measure writing ability. We give examinees Essay A and then ask Rater 1 to score the essay. Rater 1 will not give the person's exact score on Essay A. The score may be affected by Rater 1's personal biases, for example. We ask Rater 2 to score the essay as well, and we average the results. This average is closer to the examinee's actual performance on the essay. By adding raters, we can eventually exactly match the examinee's true performance on essay A. But that is not the examinee's true writing ability. That is the person's score on Essay A, which is an imperfect representation of writing ability. If we add more essays and average the scores, what we get would be a better representation of the examinee's writing ability. The more essays we add, the closer we come to measuring the examinee's true writing ability.
I could see that this formulation could help me answer many questions of interest to test builders and their clients. For example, is there an easy way to estimate the reliability of essays, especially for tests that have only one essay? Is there a tool that can help design essay tests? How many raters should score each essay? How many essays are necessary to achieve a desired reliability? Is there a simple way to understand the different sources of noise in essay tests?
The model made it easy to differentiate among multiple reliabilities, including essay observed score reliability, which is usually what we want; interrater reliability, or rater consistency; and essay true score reliability, which is the upper limit on the reliability of a particular essay. This last reliability generally has an upper bound less than 1.0. I also developed prophesy formulas for updating essay reliabilities in real time based on new information. With these formulas, which only required simple correlations, it became easier for our client to make real-world decisions, some of which were counter-intuitive. For example, Table 2 shows the writing score reliabilities for a hypothetical essay test as a function of the number of essays and the number of raters per test. We can see from the table that two essays with one rater each have higher reliability than one essay with two raters. This went against what the client thought at the time, which is that having one rater score an essay was generally unacceptable. This kind of analysis convinced the client that sometimes only one rater is fine.
The model also allowed updating the essay observed score reliability for a test with only a single essay. Often, a program faced with that situation will estimate essay reliability from a field study in which each person writes two essays. Then the resulting computed reliability will be reported for all future essays. However, given a model specifying the relationship between rater reliability and essay reliability, essay reliability can be updated based on new estimates of rater reliability.
As I forewarned, I have told a little about my background and have given just a few examples of times when I challenged my traditional thinking. I have briefly outlined some results that I achieved in the process. But what does it all mean? Let me answer this way:
Why I Don't Speak Chinese
Mandarin is a fun language to listen to and to try to learn. Initially, I thought it sounded like singing. Chinese are also very friendly people. If you visit the country and you are confused, you can walk up to a complete stranger and say, “Qǐng wèn” (请问; Excuse me). And the person will try to help you. You have to be careful, though, because Chinese is a tonal language. How you say what you say matters. If you walked up to a complete stranger and said, “Qīn wěn” (亲吻; Kiss), you might get a different reaction. But that's not why I don't speak Chinese.
No, what got me was measure words, or numerical classifiers. In English if we want to say how many, we just place a number in front of the thing: For example, three people. But in Chinese, we need to put a classifier in between: Sān gè rén; “Three things people.” Gè is a general-purpose measure word. There are different measure words for different objects. A lot of times, the measure word appears to be related to the characteristics of the object (see Table 3). For paper, the measure word is associated with flat things: In English, we would say a sheet of paper. In Chinese, it would be something like one flat thing paper. For ink pens, the measure word is associated with long, thin things: Two long thin things pens. There are hundreds of these measure words, depending on how we count. I could not keep them straight; at some point I lost hope and gave up.
| Number of Essays | |||||
|---|---|---|---|---|---|
| Number of Raters | 1 | 2 | 3 | 4 | 5 |
| 1 | .46 | .63 | .72 | .77 | .81 |
| 2 | .56 | .72 | .79 | .84 | .87 |
| 3 | .61 | .76 | .82 | .86 | .89 |
| 4 | .63 | .77 | .84 | .87 | .90 |
| 5 | .65 | .79 | .85 | .88 | .90 |
| Chinese | Pinyin | English | Measure Word Used For |
|---|---|---|---|
| 三个人 | Sān gè rén | Three people | General things |
| 一张纸 | Yī zhāng zhǐ | A sheet of paper | Flat things |
| 两支笔 | Liǎng zhī bǐ | Two pens | Long, thin things |
We can see that the categories follow a certain logic. The groupings are to a great extent culture-specific. We can tell what distinctions are important by how things are grouped. In other cultures, different things would be emphasized. For example, the Gilbert islands lie in the South Pacific right along the equator. People there live primarily by fishing, cultivating taro, and eating tree fruits. Their measure words reflect important aspects of their environment. For example, in their dialect, there are separate measure words for coconut thatch, bundles of thatch, rows of thatch, and rows of things that are not thatch (Ascher, 1998). That is because thatch is plentiful, and it is important for building. It is a central element of their culture.
Interestingly, cultures that use measure words have historically been viewed as inferior. Around the turn of the 20th century, a popular paradigm in anthropology was the theory of classical social evolution. This was the belief that cultures progress unilinearly through three basic evolutionary stages: savagery, barbarism, and civilization. All civilized societies, then, would have gone through the savagery and barbarism stages. Any societies that were still in the early stages were presumably advancing toward civilization but were not there yet (Morgan, 1877).
Anthropologists looked at different aspects of culture to find the predominant traits under each stage of cultural development. These anthropologists, who were primarily from U.S. and Western European cultures, concluded that measure words were from earlier stages of cultural development, before the concept of number was completely understood. According to these experts, someone who speaks about “three flat things paper” and “three long, thin things pens” clearly does not understand that both contain the same concept of three. And the anthropologists concluded, therefore, that such people were incapable of abstract thought (Ascher, 1998). This conclusion, unfortunately, is typical of many people when faced with a worldview different from their own.
There is not complete agreement on the origin of measure words. Some linguists believe that they are counterparts of measurements used with things that cannot be counted, such as sand. We don't have “a sand;” we have “a handful of sand,” or “a bucket of sand.” We can't talk about sand without a measure word. Or maybe measure words signal the sets to which the objects belong, or perhaps they signal to the listener the properties of the thing being counted. In any case, the measure words convey meaning by providing a link between quality and quantity of the object in question (Ascher, 1998), like good mixed methods research. There is nothing unsophisticated about that. If it were, I would have learned Chinese a long time ago.
Measurement in Context
Measurement is culture-bound, and measure words make this point clear. The structure of measure words in a particular culture tells us about their ideas about number, the structure of their language, what is important to them, and how they understand the world around them. We could take advantage of this cultural nature by beginning to measure in context. This is especially important when it comes to measuring human capabilities. We need to take people's environment into consideration when evaluating them. The idea is not new. School admissions officers have been clamoring for ways to view applicants’ scores in the context of their environment. One famous attempt was the Strivers project, which hit the media in 1999 (Gose, 1999; Marcus, 1999). The idea was simple: Instead of comparing a person's performance to the entire population, we would compare the person to their particular group. If the person exceeded the mean of their group by a specified amount, the person would be termed a Striver and would be given extra consideration. The idea was an abject failure. I think one reason for this was that Strivers was essentially trying to place an assessment from one culture into another culture and then say that the assessment had been contextualized.
Greenfield (1997) cautioned against assuming that cognitive tests transported readily across cultures. He argued that cognitive tests are rooted in social conventions in the three cultural domains of shared values, knowledge, and communication. For tests to translate from one culture to another, both cultures must share these conventions. Arguably, cognitive tests in use in the United States do not apply to every segment of the population (Randall, 2021; Walker et al., 2023). Instead of trying to place an inappropriate measurement instrument into context, we need to contextualize the measure from the beginning.
Consider, for example, two home environments traditionally linked to lower oral English skills: a lower-SES African American family and an immigrant family in which Spanish is the primary language spoken in the home. In both cases, we can expect the children from these families to have less developed standard oral English skills when they start school. In both cases, this is because the children tend to be exposed to less frequent standard English with smaller vocabularies and less complex syntactic structures than higher-SES children from English-speaking households. Because early oral language skills predict later literacy, which is an integral part of academic achievement, we can expect children from both these environments to achieve below grade level when they start school (Catts et al., 1999).
These children have other skills, however. Studies have shown that African American children are accomplished storytellers who integrate poetic devices, sound effects and movement (Gardner-Neblett, 2024; Gorman et al., 2011; Mills et al., 2013). They are good at poetic improvisation and spontaneous wit. Bilingual children show superior performance on tasks related to executive function and attentional control (Calvo & Bialystok, 2014; Morales et al., 2013). They also tend to have more advanced metalinguistic skills than monolingual children. We cannot compare these children against a single, so-called standard framework for language acquisition. If we really want to know what these children know and can do, we need to structure the assessment around their funds of knowledge rather than somebody else's lived experiences.
Expanding Our Views of Measurement
Whenever we increase our understanding of other cultures, we increase our understanding of our own by seeing what is or is not distinctive about us and by shedding more light on assumptions that we make which could, in fact, be otherwise. Our concepts of space and time ARE, after all, only our ideas and not objective truth. And, there is no single correct way to depict objects in space, nor one correct way to orient a picture in order to comprehend its contents (pp. 186–187).
A natural question at this point might be what we as individuals can do to broaden the measurement field. Perhaps the best thing we can do is to keep an open mind. If we want to raise capable leaders, we must allow them to expand beyond the confines of our own current thinking. Table 4 offers a few simple suggestions of ways to encourage students and colleagues to branch out in new directions.
| Instead of Saying… | Try This Instead… |
|---|---|
| "Not a good fit.” | “How can I help them succeed?” |
| “Stick to mainstream research.” | “Let's explore your idea.” |
| "The field will never accept that.” | “What's the best way to get this point across?” |
| “I don't do_______ research.” | “Teach me.” |
Human nature often prevents us from seeing something clearly because we are in the midst of it, which is why we need to constantly challenge our own positions. If we step back and look at things through fresh eyes, we will notice that every viewpoint has merit. In fact, we all benefit by sharing our perspectives. It gives a much more well-rounded view of the world.